Voir aussi : Du dipôle replié à l'antenne cadre - Dipôle replié sur décamétriques - Coefficient de vélocité - Dipôle replié sur VHF-

Principe

Le dipôle replié à deux tubes ou folded dipole présente, en son point d'alimentation, une impédance dont la valeur varie entre 2 et 16 fois la valeur du dipôle simple. Le coefficient multiplicateur varie en fonction du rapport des diamètres mais aussi de l'écartement des deux tubes.
Par exemple, un dipôle replié dont les tubes sont de même diamètre et qui est placé dans l'espace infini (ou du moins à plusieurs longueurs d'onde du sol et de tout élément conducteur) présente une impédance d'environ 290 ohms en son point d'alimentation, exactement 4 fois l'impédance d'un dipôle demi-onde standard. Ce coefficient multiplicateur de l'impédance est particulier car il ne varie pas en fonction de l'écartement des deux tubes (voir courbe ci-dessous).
Le dipôle replié est principalement utilisé dans les antennes yagi pour permettre une adaptation d'impédance performante. En effet, lorqu'un dipôle (le radiateur) est soumis à l'influence proche d'éléments parasites (réflecteur et directeurs), son impédance à la résonance diminue fortement jusqu'à une vingtaine d'ohms. En utilisant un dipôle replié comme radiateur on peut faire remonter cette impédance jusqu'à 75 ohms.

Trombone à deux tubes

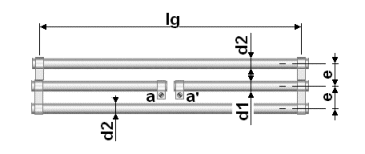
Il peut être réalisé à l'aide de deux tubes de diamètres respectifs d1 et d2 reliés entre eux à leurs extrémités par deux curseurs conducteurs. La distance e entre les deux tubes est mesurée d'axe à axe.


Calcul du coefficient multiplicateur

La formule permettant de calculer le coefficient k est la suivante :

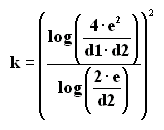
Les trois dimensions doivent être exprimées dans la même unité, quelque qu'elle soit (mm,cm ou m). On pourra utiliser avantageusement le tableur d'OpenOffice pour programmer la formule.

Impédance en fonction du diamètre des tubes (dipôle à deux tubes)

Lorsque les diamètres d1 et d2 sont égaux, l'impédance à la résonance au point d'alimentation de l'antenne dans l'espace est de l'ordre de 290 ohms, soit 4 fois celle d'un dipôle simple. Ce coefficient multiplicateur de 4 n'est valable que pour des tubes identiques et peut varier entre 2 et 14 en fonction du rapport d2/d1 et e/d2. L'intérêt de cette possibilité est l'adaptation de l'impédance au point d'alimentation d'une antenne yagi en utilisant un dipôle replié comme radiateur. 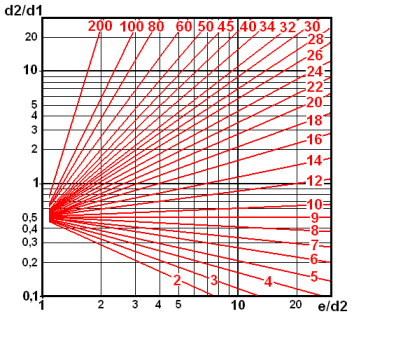Comme la présence des éléments parasites abaisse l'impédance du radiateur, il est possible de remonter cette impédance à 50 ou 75 ohms pour pouvoir alimenter l'antenne avec un câble coaxial d'impédance courante.
L'abaque ci-contre permet de déterminer rapidement le coefficient multiplicateur en fonction de e, d1 et d2. Il suffit de déterminer auparavant les rapports e/d2 et d2/d1.
Exemple :
Un trombone est formé de deux tubes espacés de 48 mm et de diamètres d2=12, d1=6.
e/d2=4
d2/d1=2
On peut lire sur le graphe que le point correspondant est situé entre les droites bleues 5 et 6 donc que le coefficient multiplicateur k est d'environ 5,5 (5,44 exactement). Isolé dans l'espace, ce dipôle replié présenterait une impedance de 75x5,44=408 ohms.
Ces valeurs sont bien sûr théoriques. Quand on expérimente réellement sur les antennes on constate que les valeurs mesurées sont souvent différentes.



Dipôle replié à 3 tubes

Pour obtenir des impédances plus élevées, il est possible d'associer trois tubes comme sur la figure ci-contre. L'élément alimenté doit se trouver au centre, les deux autres tubes ont un diamètre identique et sont espacés d'une même distance e du tube central.

Impédance du dipôle à 3 tubes

Dans le dipôle replié à 2 tubes relié à un générateur, le courant I produit par la puissance P du générateur se répartit dans les deux tubes de façon identique si ceux-ci ont le même diamètre. La résistance de rayonnement R entre a et a' est égale à P/(I/2)² et 4 fois plus grande que le dipôle simple. Pour un dipôle à 3 tubes, cette résistance R est égale à P/(I/3)². Elle est de ce fait 9 fois plus élevée que celle d'un dipôle simple placé dans les mêmes conditions.
L'abaque ci-contre permet d'estimer la valeur du coefficient multiplicateur en fonction des e, d1 et d2. Attention, ces valeurs théoriques ne sont pas toujours possibles dans la réalité.