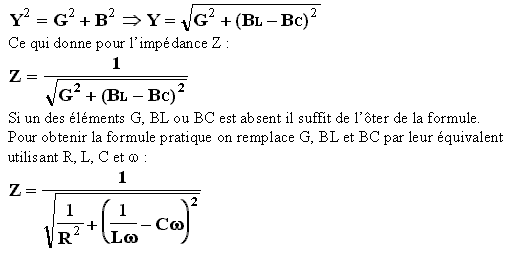Voir aussi : Impédance d'une bobine - la réactance - Application du tableur : formule de Thomson - Le circuit série LC à la résonance - Impédance - Le circuit bouchon, circuit résonant parallèle - Le coefficient de surtension d'un circuit bouchon - Sélectivité et bande passante d'un circuit - L'abaque de Smith -


Le circuit RLC parallèle

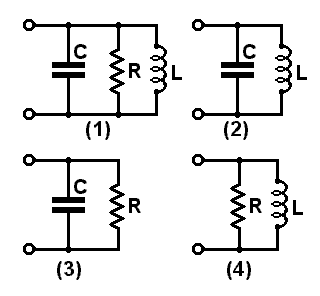
Il se compose d'une résistance R, d'un condensateur C et d'une self L branchés en parallèle. Il arrive que l'un de ces trois éléments manque ou soit négligeable : on peut donc rencontrer quatre cas symbolisés sur la figure ci-contre. Exemples :
(1) circuit bouchon amorti par une résistance pour diminuer sa sélectivité.
(2) circuit bouchon idéal
(3) circuit RC
(4) self shuntée par une résistance.
Dans ces quatre cas les composants sont considérés comme parfaits : les connexions n'ont pas d'inductance, il n'y a pas de capacités parasites entre les composants, le condensateur n'a pas de pertes et la self a une résistance nulle.

Calcul de l'impédance d'éléments en parallèle

La résistance équivalente à deux ou plusieurs résistances pures R en parallèle peut se calculer avec la formule :

La méthode est identique pour des réactances :

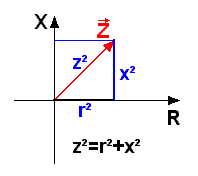Par contre R et X se trouvant sur des axes différents (voir figure ci-contre) il n'est pas possible d'utiliser exactement la même formule, c'est pourquoi Z (l'hypoténuse du triangle rectangle dont les autres côtés sont X et R) doit être calculée à l'aide du théorème de Pythagore.
Lorsque plusieurs éléments résistifs et réactifs sont branchés en parallèle on commence par calculer la réactance X équivalente aux éléments réactifs en affectant par convention un signe - aux réactances capacitives et un signe + aux réactances selfiques puis la résistance R équivalente aux éléments résistifs. On peut alors calculer l'impédance du circuit à l'aide de la formule :



Cas de deux éléments en parallèle
Prenons l'exemple du circuit (4) comportant une résistance R en parallèle avec une bobine (supposée parfaite) d'inductance L.



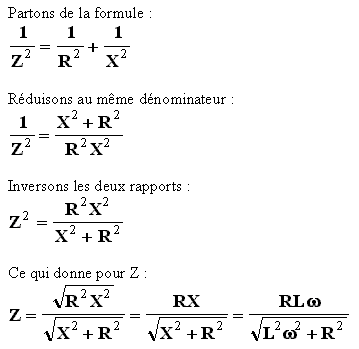
Utilisation des conductance, admittance et susceptance

On a intérêt à utiliser cette méthode lorsque qu'il y a plus de deux éléments en parallèle.
La conductance G (en mho) est l'inverse de la résistance R (en ohm).
L'admittance Y (en siemens) est l'inverse de l'impédance Z (en ohm).
La susceptance B (en siemens) est l'inverse de la réactance X (en ohm).
Ces grandeurs sont utilisées pour faciliter les calculs d'éléments en parallèle. Ainsi la formule ci-dessus peut être écrite :


Exemple : calcul de l'impédance du circuit parallèle RLC

La méthode suivante peut être utilisée pour chacun des circuits schématisés ci-dessus.
La susceptance B est la somme des susceptances en affectant le signe - aux susceptances capacitives.