Voir aussi : La loi d'Ohm, générateurs de courant continu

Problème complexe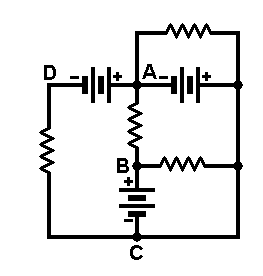

Le circuit de la figure ci-jointe (pur exemple) montre un circuit complexe formé de générateurs et de charges débitant les uns dans les autres. En plus de la loi d'Ohm, deux lois de Kirchhoff peuvent aider le calcul des intensités dans chaque élément ou la différence de potentiel entre deux points du circuit.
- Les points de convergence A ou B sont appelés des noeuds.
- La portion de circuit A-B-C-D est appelée une maille
- Une branche est une portion de circuit délimitée par deux noeuds (ex : AD ou BC).

Première loi de Kirchhoff

Considérons un noeud X sur lequel sont reliés 5 branches. Un courant parcourt chaque branche en se dirigeant vers le noeud (i1, i3 et i4) ou en s'en éloignant (i2 et i5). Comme l'électricité ne peut s'arrêter en un point d'un circuit, on peut dire que la somme des courants qui se dirigent vers un noeud est égale à la somme des courants qui s'en éloignent. Ou encore :
La somme algébrique des intensités des courants qui passent par un noeud est nulle.
Lors du calcul on convient que les courants qui se dirigent vers le noeud ont un signe "+" et ceux qui s'en éloignent un signe "-"

Deuxième loi de Kirchhoff

Dans un circuit en forme de boucle comme celui de la figure ci-jointe, si l'on additionne les tensions aux bornes de chacun des éléments du circuit on obtient un résultat égal à zéro. Pour obtenir ce résultat il faut bien sûr tenir compte de la polarité des tensions en choisissant un sens conventionnel. On prendra, par exemple, comme référence la polarité de E3. Les tensions U1 et U2 aux bornes des résistances R1 et R2 sont considérées comme de polarités inverses à celle de E3. Ce qui permet d'écrire :
E3-U1-E4-U2=0
Ce raisonnement peut être utilisé dans tout circuit fermé composé de 2, 3, 4... éléments passifs (résistance...) ou actifs (pile...) reliés en série. En outre il ne faut pas perdre de vue que l'intensité du courant est la même dans chaque élément du circuit.
La seconde loi de Kirchhoff s'énonce :
"Dans un circuit fermé (une maille) la somme algébrique des forces électromotrices et des différences de potentiel aux bornes des résistances est nulle"