Les signaux périodiques que nous utilisons, que ce soit en basse ou en haute fréquence, sont rarement purement sinusoïdaux. Ils sont en fait un mélange de signaux sinusoïdaux dont les fréquences respectives sont multiples de la fréquence fondamentale, la fréquence la plus basse. Ces fréquences multiples de la fréquence fondamentale sont appelés harmoniques.

Les harmoniques

Soit un signal de fréquence fondamentale 440 hertz (le la3 du piano). Ses harmoniques sont :
- 880 Hz harmonique 2 - la4
- 1320 Hz harmonique 3 - la5
- 1760 Hz harmonique 4 - la6
- 2200 Hz harmonique 5 - la7
- 2640 Hz harmonique 6 - la8
- 3080 Hz harmonique 7 - la9
On distingue souvent les harmoniques pairs et impairs.

Le timbre d'un signal audible

La même note la3 jouée sur un instrument de musique à vent (trompette, flute...) et sur un instrument à cordes (violon, clavecin...) ne rend pas du tout le même son. Pourtant la fréquence fondamentale est la même : 440 Hz. Ce qui fait la différence entre les deux sons est la proportion d'harmoniques. Un son assourdi est pauvre en harmoniques, un son brillant en comporte beaucoup.

Les harmoniques en émission radio

Un des moyens pour multiplier la fréquence d'un signal est de le faire passer par un étage non linéaire, un amplificateur saturé par exemple. Il suffit ensuite de filtrer le signal complexe pour en extraire l'harmonique souhaité. C'est l'aspect intéressant des harmoniques.
A l'opposé, un signal HF chargé d'harmoniques trop importants est cause de brouillage. A la sortie d'un émetteur on placera un filtre passe-bas dont la fréquence de coupure sera choisie entre la fréquence fondamentale et l'harmonique 2.

La présence d'harmonique 3

Sur la figure ci-contre, la courbe (a) montre un signal f de fréquence fondamentale et d'amplitude 1 et un signal H3 de fréquence 3 fois plus élevé que la fréquence de f et d'amplitude 0,1.
La courbe (b) représente le signal résultant de l'addition point par point des deux courbes f et H3. La distorsion est importante.


Le signal carré

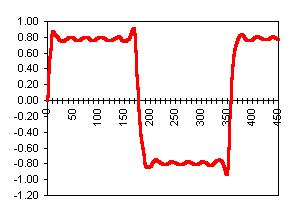Le signal représenté sur la courbe ci-contre ressemble fortement à un signal carré. Il a en fait été reconstitué à l'aide d'une partie des composantes d'un signal carré : une fréquence fondamentale et ses harmoniques impaires. Chaque composante a une amplitude particulière :
- fondamentale : amplitude 1
- harmonique 3 : amplitude 1/3
- harmonique 5 : amplitude 1/5
-harmonique 7 : amplitude 1/7
...et ainsi de suite jusqu'à l'harmonique 23.
Pour obtenir un signal parfaitement carré, il aurait fallu une infinité d'harmoniques.
Si les harmoniques pairs avaient été choisis à la place des harmoniques impairs, la forme du signal résultant aurait été un triangle. La musique synthétique est fabriquée à l'aide du même procédé.


Analyse spectrale

La représentation du signal carré ci-dessus est une courbe des variations d'amplitude en fonction du temps. Elle ne permet pas de se faire une idée des harmoniques le composant. Pour ce faire il faut observer le signal à l'aide d'un analyseur de spectre, appareil permettant d'afficher sur un écran l'amplitude des composantes d'un signal en fonction de la fréquence. L'image obtenue ressemble au graphe ci-contre. Elle correspond à une décomposition en série de Fourier du signal carré.